Break-even-Analyse
by Clemens Werkmeister
Idea of break-even-analyses
A break-even-point (or break-even-volume) is a point at which the positive effects of a decision (typically sales revenues) cover the negative effects (typically costs). This critical point is interesting if both the positive and the negative effects depend to a different extent on a common factor (e. g. production volume or activity) whose value is unknown. In this case it is not possible to calculate the profit of the decision. Instead, the break-even-point answers the question above which value of the common factor the decision will lead to higher positive than negative effects, or (to put it simple) above which value we will make profit.
The relations between costs, sales revenues, profits and the unknown or uncertain common factor are the objects of break-even-analyses or cost-volume-profit-(CVP)-analyses.
Given the broad variety of decisions with positive and negative effects in business and daily life, and the uncertainty we often face with respect to important factors, break-even-analyses have a long tradition in controlling and management. Apart from earlier anecdotic evidence, we find first formal approaches in the 19th century. Schweitzer/Troßmann (1986, 1998) provide an excellent overview and detailed descriptions of numerous specific variants and extensions of break-even-analyses for very different situations. In the following, we present the basic model and an extension to the multi-product case.
The standard model of break-even-analysis
Calculation of the break-even-point in the standard model
In standard break-even-analysis, sales revenues and costs both depend in linear, but different ways on production volume (or sales volume) as a single common factor. Sales revenues are assumed to be simply unit price (p) times production volume (x). Total costs are the sum of fixed costs (Kf, which do not depend on production volumes) and variable costs (Kv) which are calculated as variable cost per unit (kv) times the number of units (or production volume) x.
- E(x) = p • x
- K(x) = Kf + Kv(x) = Kf + kv • x
Both sales and costs depend on the production volume. The break-even-point is the volume which results in the same costs and sales revenues.
- E(x) = K(x) or p • x = Kf + kv • x
This simple condition results in the break-even-volume:
- x* = Kf/(p – kv).
Standard break-even-analysis using contribution margins
Sometimes, the break-even-volume is computed in a slightly different way using total and unit contribution. Unit contribution (d) (or contribution margin) is the difference between sales price and variable or direct costs per unit; total contribution (D) is unit contribution times the production volume:
- d = p - kv
- D(x) = d • x
The break-even point corresponds to the condition D(x) = Kf:
- x* = Kf/d.
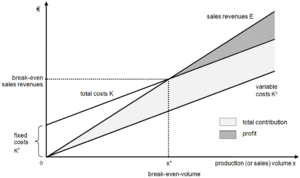
Graphical break-even-analysis
An important appeal of break-even-analyses comes from its intuitive graphical presentation. The following graph shows the standard model of break-even-analysis.
Assumptions of standard break-even analysis
Both ways of the standard break-even-analysis are designed for quite simple problems (cp. Schweitzer/Troßmann 1998, pp. 38 ff.):
- The model assumes a simple production structure with one product. Convergent production is possible if the production coefficients are fixed. Divergent or multi-product cases require more challenging approaches.
- Assumptions concerning costs and sales revenues:
- Cost and sales revenues depend only on the same single factor, the volume, number of units or activity which can be measured by a continuous variable. Other factors are assumed to be constant, irrelevant of covered by the volume, too.
- Cost and sales revenues are linear but different. Non-linear or step-wise linear cost and sales revenue functions resulting, among others, from intensity effects, discrete capacity increases or volume discounts are more difficult to handle.
- It is possible to separate costs into a fixed and a variable part. Without this cost separation, the break-even-volume would be zero (if p ≥ k) or there wouldn’t be any break-even point at all (if p < k).
- Financial goals, especially costs recovery, are important for the company.
- All input data except the volume x are known.
- The problem is short-term. This means that there is no need for distinguishing different dates of payments and discounting future values.
Dealing with different assumptions in break-even-analysis
These assumptions limit the use of break-even-analyses to a very narrow range of cases. For other cases, Schweitzer/Troßmann (1998) describe variants and extensions of the standard break-even model.
- Variants of break-even-analysis include (see Schweitzer/Troßmann 1998, pp. 55 ff.):
- Separate break-even-points for different levels of financial goals. It is straightforward to calculate increasing break-even-points corresponding to a zero EBITDA, a zero EBIT, zero earnings or other target earnings.
- Cost-volume-profit-analyses (in the narrow sense of the term) look at the reaction of the break-even-point on variations of unit prices, unit variable costs, or the fixed costs. A typical application is the configuration of a product through value engineering.
- Differences between production and sales volumes can be modeled through the introduction of inventories.
- Instead of comparing sales and costs of one project or technique, costs for different projects or techniques to manufacture the same product can be analyzed. Typical applications include decisions about rationalization, the choice among alternative plants, or technological innovations. The result is a recommendation whether to shift from one technique to the next, and a break-even-point for this technology shift.
A common characteristic of these variants is that they calculate the break-even-points in the same ways as in the standard model. In general, finding the relevant information or simplifying it to fit to the assumptions of standard break-even analyses is more difficult than its use.
- Extensions of break-even-analyses
- Extensions of break-even-analyses override the limits or the simplifications of the standard model. They require different computational approaches to determine the break-even-points. The most important extensions deal with (see Schweitzer/Troßmann 1998, pp. 122 ff.):
- non-linear production structures, especially for divergent or regrouping multi-product cases
- non-linear cost and sales functions
- more than one factor, especially the multi-product cases or the combination of output units with process conditions (temperature, ...)
- dynamic production processes, especially multi-period processes and inventories
- multiple goals.
In order to deal with these kinds of situations, both simplifying and more sophisticated mathematical methods, mainly linear or mixed-integer vector or matrix programming methods, have been presented.
Dealing with risk in break-even-analyses
Break-even-analysis itself is a technique designed to deal with one form of uncertainty: the uncertain outcome of the production or sales volume. The other input data of the break-even model (unit prices, unit variable costs, fixed costs, …) are deterministic. However, if additional information is available, further insights are possible. The additional information can consist in:
- the expected value xe of sales volume: this information allows to calculate the following margin of safety S (cp. Tucker 1963):
- S = (xe – x*)/xe
The higher the margin of safety, the more the actual sales volume can fall short of the expected volume without causing a loss. This is a simple but rather chunky way to capture the uncertainty.
- a probability distribution of sales volume: based on this information it is possible to calculate measures as probabilities of erroneous decisions, risk-chance-relations, risk-levels, expected uncertainty costs which have been presented in the literature(for an detailed overview see Schweitzer/Troßmann (1998), pp. 97-123).
- probability distributions of other input data: this information can be used in stochastic approaches to break-even-analyses that provide probability distributions for the break-even-point (see Schweitzer/Troßmann (1998), pp. 307-333). Given the stochastic prices, variable or fixed costs, even in the case of known (deterministic) sales volume, it is uncertain whether the project results in a profit or a loss.
Benefits of break-even-analyses
Starting from the quite intuitive standard break-even-model, numerous variants and extensions have been suggested. Sometimes a more sophisticated approach might be seen as a “methodological overkill” and a simpler approach may be sufficient. This trade-off depends largely on the situation and, properly used, break-even-analyses are among of the most important tools of controlling and managerial accounting.
However, the broad acceptance of break-even-analyses in everyday business situations goes beyond the calculation of break-even-points. It is due to the fact that even simple approaches require an analysis of the critical factors that influence sales, cost and profits, and of the way they do it – exactly the information every manager would like to have.
---
see too: Multi-product break-even-analysis
References:
Schweitzer, M.; E. Troßmann; G. E. Lawson: Break-even-Analyses. John Wiley & Sons 1992.
Schweitzer, M.; E. Troßmann: Break-even-Analysen. 2. Aufl., Berlin 1998 (1. Aufl. 1986).
Tucker, Spencer A.: The Break-Even System: A Tool for Profit Planning. Englewood Cliffs (N J.) 1963.