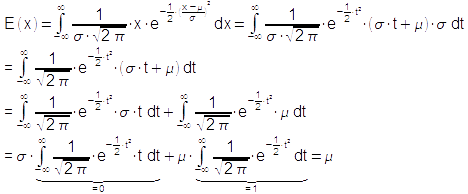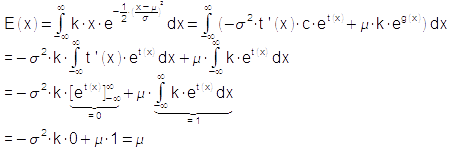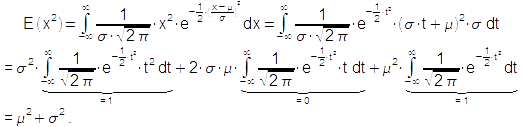Erwartungswert einer normalverteilten Zufallsvariablen: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „Der Erwartungswert einer normalverteilten Zufallsvariablen x (mit x ~ N(μ; σ²) mit Dichtefunktion f(x) wird wie folgt definiert: [[Datei:Ewert_NV_01.pn…“) |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
In zahlreichen betriebswirtschaftlichen Anwendungen wird eine normalverteilte Zufallsvariable unterstellt. Hier wird die Berechnung der beiden zentralen [[Risikokennzahl|Risikokennzahlen]] Erwartungswert und Varianz für diesen Verteilungstyp erläutert. | |||
==Berechnung des Erwartungswerts== | |||
Der Erwartungswert einer normalverteilten Zufallsvariablen x (mit x ~ N(μ; σ²) mit Dichtefunktion f(x) wird wie folgt definiert: | Der Erwartungswert einer normalverteilten Zufallsvariablen x (mit x ~ N(μ; σ²) mit Dichtefunktion f(x) wird wie folgt definiert: | ||
[[Datei:Ewert_NV_01.png]] | [[Datei:Ewert_NV_01.png]] | ||
Zur | Zur Vereinfachung substituiert man den Exponenten der Exponentialfunktion [[Datei:Ewert_NV_10.png]] mit [[Datei:Ewert_NV_11.png]] und [[Datei:Ewert_NV_12.png]]. Zudem verwendet man die Zerlegung [[Datei:Ewert_NV_13.png]]. Dann lautet der gesuchte Erwartungswert: | ||
[[Datei:Ewert_NV_05.png]] | |||
Einsetzen in die Definitionsgleichung und Umformen führt zu: | |||
[[Datei:Ewert_NV_15.png]]. | |||
[[Datei: | ==Alternative Berechnung des Erwartungswerts== | ||
Einen ähnlichen Weg zur Integralberechnung erhält man mit [[Datei:Ewert_NV_03.png]] und [[Datei:Ewert_NV_04.png]], der Zerlegung [[Datei:Ewert_NV_06.png]] sowie der Substitution des konstanten Ausdrucks [[Datei:Ewert_NV_02.png]]. Mit ihnen erhält man den Ausdruck | |||
[[Datei:Ewert_NV_07.png]]. | |||
und bildet das gesuchte Integral über die zerlegte Form. Nach den nötigen Umformungen ergibt sich der Erwartungswert μ: | und bildet das gesuchte Integral über die zerlegte Form. Nach den nötigen Umformungen ergibt sich der Erwartungswert μ: | ||
| Zeile 16: | Zeile 28: | ||
[[Datei:Ewert_NV_09.png]]. | [[Datei:Ewert_NV_09.png]]. | ||
==Berechnung der Varianz== | |||
Die Berechnung der Varianz erfolgt am einfachsten als Differenz: σ² = E(x)² – E(x²): | |||
Dazu ist der Erwartungswert E(x²) zu berechnen. Dies geschieht analog zur Berechnung von E(x): | |||
[[Datei:Ewert_NV_16.png]] | |||
Damit gilt für die Varianz: | |||
[[Datei:Ewert_NV_17.png]]. | |||
___<br> | |||
siehe auch:<br> | |||
Ruhm, Karl H.: Kennwerte der Normalverteilung. Internet-Portal "Wissenschaft und Technik des Messens"; Dokument: http://www.mmm.ethz.ch/dok01/d0000411.pdf. | |||
Version vom 11. Mai 2011, 14:42 Uhr
In zahlreichen betriebswirtschaftlichen Anwendungen wird eine normalverteilte Zufallsvariable unterstellt. Hier wird die Berechnung der beiden zentralen Risikokennzahlen Erwartungswert und Varianz für diesen Verteilungstyp erläutert.
Berechnung des Erwartungswerts
Der Erwartungswert einer normalverteilten Zufallsvariablen x (mit x ~ N(μ; σ²) mit Dichtefunktion f(x) wird wie folgt definiert:
Zur Vereinfachung substituiert man den Exponenten der Exponentialfunktion ![]() mit
mit ![]() und
und ![]() . Zudem verwendet man die Zerlegung
. Zudem verwendet man die Zerlegung ![]() . Dann lautet der gesuchte Erwartungswert:
. Dann lautet der gesuchte Erwartungswert:
Einsetzen in die Definitionsgleichung und Umformen führt zu:
Alternative Berechnung des Erwartungswerts
Einen ähnlichen Weg zur Integralberechnung erhält man mit ![]() und
und ![]() , der Zerlegung
, der Zerlegung ![]() sowie der Substitution des konstanten Ausdrucks
sowie der Substitution des konstanten Ausdrucks ![]() . Mit ihnen erhält man den Ausdruck
. Mit ihnen erhält man den Ausdruck
und bildet das gesuchte Integral über die zerlegte Form. Nach den nötigen Umformungen ergibt sich der Erwartungswert μ:
wegen
Berechnung der Varianz
Die Berechnung der Varianz erfolgt am einfachsten als Differenz: σ² = E(x)² – E(x²): Dazu ist der Erwartungswert E(x²) zu berechnen. Dies geschieht analog zur Berechnung von E(x):
Damit gilt für die Varianz:
___
siehe auch:
Ruhm, Karl H.: Kennwerte der Normalverteilung. Internet-Portal "Wissenschaft und Technik des Messens"; Dokument: http://www.mmm.ethz.ch/dok01/d0000411.pdf.