Financial Resources Formulary: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 3: | Zeile 3: | ||
== | == Present values, perpetuities and annuities == | ||
'''Present value PV:''' value of a future payment C<sub>t</sub> (in year t), discounted to year 0: [[Datei:Form_FV.png]] | '''Present value PV:''' value of a future payment C<sub>t</sub> (in year t), discounted to year 0: [[Datei:Form_FV.png]] | ||
| Zeile 52: | Zeile 52: | ||
'''Annual percentage rate (APR) or simple rate:''' annualized rate of shorter period interest rates (monthly, daily rates) using simple interest. | '''Annual percentage rate (APR) or simple rate:''' annualized rate of shorter period interest rates (monthly, daily rates) using simple interest. | ||
:- APR for a monthly rate m: APR = 12 m | :- APR for a monthly rate m: APR = 12 * m | ||
Given an annual percentage rate (APR) of r, the corresponding EAR with respect to n shorter periods of equal length is: | Given an annual percentage rate (APR) of r, the corresponding EAR with respect to n shorter periods of equal length is: [[Datei:Form_EAR.png]] | ||
'''Effective annual rate with continuous compounding:''' effective annual rate for n → ∞ shorter periods | '''Effective annual rate with continuous compounding:''' effective annual rate for n → ∞ shorter periods: [[Datei:Form_EAR_cc.png]] (being r the simple annual rate) | ||
(being r the simple annual rate) | |||
'''Real rate of return:''' rate of return adjusted for inflation | '''Real rate of return:''' rate of return adjusted for inflation: [[Datei:Form_Real_Int_1.png]] | ||
→ | → [[Datei:Form_Real_Int_2.png]] (being i the inflation rate) | ||
| Zeile 66: | Zeile 65: | ||
== Valuing bonds == | == Valuing bonds == | ||
'''Price of a bond:''' | '''Price of a bond:''' [[Datei:Form_PV_Bond.png]] | ||
| Zeile 75: | Zeile 74: | ||
: N maturity<br/> | : N maturity<br/> | ||
'''Duration of a bond with maturity N:''' weighted average period of bond payments. | '''Duration of a bond with maturity N:''' weighted average period of bond payments: [[Datei:Form_Duration.png]] | ||
'''Modified duration:''' a measure of volatility (elasticity) of bond prices: | '''Modified duration:''' a measure of volatility (elasticity) of bond prices: [[Datei:Form_Mod_Duration.png]] | ||
| Zeile 83: | Zeile 82: | ||
== Valuing stocks == | == Valuing stocks == | ||
'''(Expected) [[Wertpapierrendite|Stock return r]] (equity cost of capital):''' | '''(Expected) [[Wertpapierrendite|Stock return r]] (equity cost of capital):''' [[Datei:Form_Stock_Return.png]] | ||
'''Stock price P<sub>0</sub> in the single-period case:''' | '''Stock price P<sub>0</sub> in the single-period case:''' [[Datei:Form_P0_einperiodig.png]] | ||
'''Dividend discount model''' for the stock price P0 in the multi-period case until time horizon H: | '''Dividend discount model''' for the stock price P0 in the multi-period case until time horizon H: [[Datei:Form_P0_mehrperiodig.png]] | ||
'''Stock price P<sub>0</sub>''' with specific dividends until time horizon H and growing dividends after H: | '''Stock price P<sub>0</sub>''' with specific dividends until time horizon H and growing dividends after H: [[Datei:Form_P0_growth.png]] | ||
'''Stock price for a perpetual stream of dividends:''' | '''Stock price for a perpetual stream of dividends:''' [[Datei:Form_P0_perpetual.png]] | ||
'''Stock price for a perpetual stream of growing dividends:''' | '''Stock price for a perpetual stream of growing dividends:''' [[Datei:Form_P0_perp_growth.png]] | ||
'''Return (Equity cost of capital) of a perpetual stream of dividends with growth:''' | '''Return (Equity cost of capital) of a perpetual stream of dividends with growth:''' [[Datei:Form_RoE_growth.png]] | ||
'''Return on Equity with market values:''' | '''Return on Equity with market values:''' [[Datei:Form_RoE.png]] | ||
'''Payout ratio:''' fraction of earnings paid out as dividends: | '''Payout ratio:''' fraction of earnings paid out as dividends: [[Datei:Form_Payout.png]] | ||
'''Plowback ratio:''' fraction of earnings retained by the firm: | '''Plowback ratio:''' fraction of earnings retained by the firm: [[Datei:Form_Plowback.png]] | ||
'''Present value of growth opportunities (PVGO):''' net present value of a firm's future investments | '''Present value of growth opportunities (PVGO):''' net present value of a firm's future investments. | ||
'''Sustainable growth rate:''' rate at which a firm can steadily grow: | '''Sustainable growth rate:''' rate at which a firm can steadily grow: [[Datei:Form_Sustainable.png]] | ||
'''Discounted cash flow (DCF):''' value of the free cash flows that are available to investors plus company value at the planning horizon, all discounted to present: | '''Discounted cash flow (DCF):''' value of the free cash flows that are available to investors plus company value at the planning horizon, all discounted to present: [[Datei:Form_DCF.png]] | ||
| Zeile 151: | Zeile 150: | ||
== | == Capital Structure and Return == | ||
'''[[Rentabilität|Rates of return]]:''' | '''[[Rentabilität|Rates of return]]:''' | ||
Version vom 3. Dezember 2011, 15:03 Uhr
by Clemens Werkmeister
Present values, perpetuities and annuities
Present value PV: value of a future payment Ct (in year t), discounted to year 0: ![]()
Future value FVt: value of a present payment (in year 0), calculated by compounding to year t: ![]()
- t year
- r discount rate (interest rate)
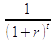 discount factor with discount rate (interest rate) r for t years
discount factor with discount rate (interest rate) r for t years- Ct cash flow in year t
- C0 initial investment of a project (for normal investment projects: C0 < 0)
- T number of years of the project
The sum of several present values is a PV, too (additivity of present values):![]()
Net present value NPV: PV of future payments (of a project or a company) plus the - usually negative - initial investment C0: ![]()
Perpetuity (console): a periodic (annual) payment C that is received or paid forever (beginning with the first payment at the end of year 1):![]()
Annuity: a payment of a level cash flow C during a specified number of years (from year 1 to n). Its present value can be calculated as difference between two perpetuities: ![]()
Annuity (recovery) factor: average payment at the end of n periods, corresponding to a present value PV and considering for interest rate r:![]()
Annuity present value factor: factor for the PV of n equal payments at the end of years 1 to n: ![]()
The annuity C for years 1 to n corresponding to a present value PV and discount rate r is: ![]()
Growing perpetuity: a perpetuity starting with cash flow C1 in year 1 and increasing by the annual growth rate g forever:![]() (for t = 1, 2, …, ∞ ;g < r) and
(for t = 1, 2, …, ∞ ;g < r) and ![]()
Growing annuity: an annuity starting with cash flow C1 in year 1 and increasing by the annual growth rate g for n years: ![]() (with t = 1, 2, …, n)
(with t = 1, 2, …, n)
Internal rate of return (IRR): discount rate that results in NPV = 0: ![]()
Profitability index: ratio of NPV to investment of a project: ![]()
Equivalent annual cash flow (EAC): cash flow per year with the same present value as the actual cash flow of the project: 
Interest and discount rates
Effective annual rate (EAR): annualized rate of shorter period interest rates (monthly, daily rates) using compound interest:
- - EAR for a monthly rate m: EAR = (1+m)12 – 1
- - EAR for a daily rate d: EAR = (1+d)360 – 1 (for 360 days per year)
Annual percentage rate (APR) or simple rate: annualized rate of shorter period interest rates (monthly, daily rates) using simple interest.
- - APR for a monthly rate m: APR = 12 * m
Given an annual percentage rate (APR) of r, the corresponding EAR with respect to n shorter periods of equal length is: ![]()
Effective annual rate with continuous compounding: effective annual rate for n → ∞ shorter periods: ![]() (being r the simple annual rate)
(being r the simple annual rate)
Real rate of return: rate of return adjusted for inflation: ![]() →
→ ![]() (being i the inflation rate)
(being i the inflation rate)
Valuing bonds
with
- Ct annual coupon interest payment
- F face value (or principal)
- r discount rate (yield to maturity)
- N maturity
Duration of a bond with maturity N: weighted average period of bond payments: 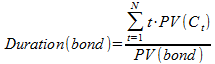
Modified duration: a measure of volatility (elasticity) of bond prices: ![]()
Valuing stocks
(Expected) Stock return r (equity cost of capital): ![]()
Stock price P0 in the single-period case: ![]()
Dividend discount model for the stock price P0 in the multi-period case until time horizon H: ![]()
Stock price P0 with specific dividends until time horizon H and growing dividends after H: ![]()
Stock price for a perpetual stream of dividends: ![]()
Stock price for a perpetual stream of growing dividends: ![]()
Return (Equity cost of capital) of a perpetual stream of dividends with growth: ![]()
Return on Equity with market values: ![]()
Payout ratio: fraction of earnings paid out as dividends: ![]()
Plowback ratio: fraction of earnings retained by the firm: ![]()
Present value of growth opportunities (PVGO): net present value of a firm's future investments.
Sustainable growth rate: rate at which a firm can steadily grow: 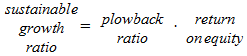
Discounted cash flow (DCF): value of the free cash flows that are available to investors plus company value at the planning horizon, all discounted to present: ![]()
Risk and return
Risk premium of an asset: asset return – return of risk-free asset
Variance: expected value of squared deviations of observations from their expected value (mean):
based on j observations
Standard deviation: a measure of volatility of expected stock returns:
Expected portfolio return (with two assets):
Expected portfolio return (with j = 1, …, n assets):
- xj weight of asset j in the portfolio
- rj (expected) return of asset j
Variance of portfolio return (portfolio variance) in the case of two assets:
Covariance between asset i and j with
Correlation coefficient between asset i and j:
Variance of portfolio return (portfolio variance) in the case of n assets:
Beta of the return of asset j to the market return (return of market portfolio m):
Expected return following the security market line equation (SML):
Expected return of a stock in event studies:
Abnormal return = actual return – expected return =
Capital Structure and Return
Weighted average cost of capital (WACC):
- rD interest rate on debt resp. debt cost of capital
- rE return on equity resp. equity cost of capital
- Tc corporate tax rate
Weighted average cost of capital (WACC) with a zero-tax rate:
Leverage-formula for return on equity: return on equity increases with debt/equity-ratio
Leverage-formula for equity beta: risk increases with debt/equity-ratio: