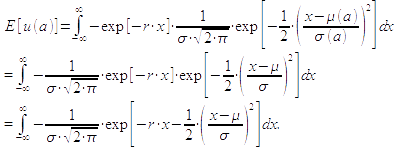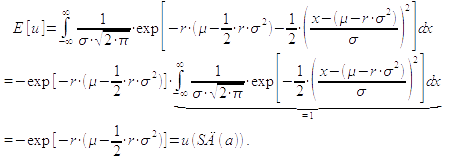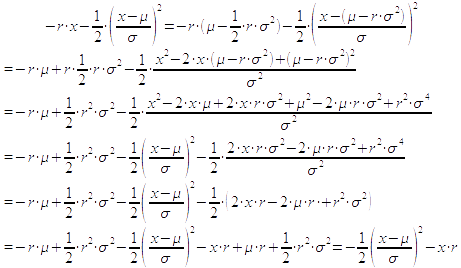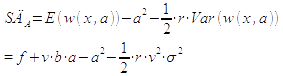Sicherheitsäquivalent bei exponentieller Nutzenfunktion

Wichtige betriebswirtschaftliche Entscheidungs- und Anreizmodelle nutzen die rechentechnischen Vorteile aus, die bestimmte Risikonutzenfunktionen und Annahmen zur Wahrscheinlichkeitsverteilung bieten. Eine rechentechnisch besonders vorteilhafte Kombination liegt bei exponentieller Risikonutzenfunktion und normalverteilter Zufallsvariablen vor, da sie eine einfache geschlossene Berechnung des Sicherheitsäquivalents erlaubt. Auf dieser Kombination beruht bspw. das LEN-Modell der Prinzipal-Agenten-Theorie.

Herleitung des Sicherheitsäquivalents

Eine exponentielle Nutzenfunktion u(x) = -exp(-r · x) bezüglich der Zufallsvariablen x weist eine konstante absolute Risikoaversion r auf. Sie gehört damit zur Klasse der CARA-Risikonutzenfunktion (CARA = Constant absolute risk aversion). Für diese Nutzenfunktion lässt sich bei normalverteilter Zufallsvariable x als Ergebnisgröße das Sicherheitsäquivalent in besonders einfacher Form ausdrücken. Dies gilt auch, wenn die Ergebnis­größe x(a) linear in Abhängigkeit einer Einflussgröße a (bspw. der Anstrengung) und eines normalverteilten Störterms e mit Erwartungswert null und Varianz σ² ausgedrückt werden kann. Setzt man

mit und damit wegen E(b · a) = μ(a) auch ,

dann bestimmt sich das Sicherheitsäquivalent (Certainty Equivalent) der exponentiellen Nutzenfunktion aus dem Erwartungswert des Ergebnisses abzüglich einer Risikoprämie:

.

Das Ausmaß der Risikoprämie hängt von der Risikoaversion der Nutzenfunktion (gemessen durch das Arrow-Pratt-Risikomaß r) sowie der Varianz des Ergebnisses ab.

Die Herleitung des Sicherheitsäquivalents beruht darauf, dass der Erwartungsnutzen E[u(a)] gleich dem Nutzen des Sicherheitsäquivalents u(SÄ(a)) ist. Für den erwarteten Nutzen E[u(a)] in Abhängigkeit der Anstrengung a gilt (zur übersichtlicheren Darstellung werden im Folgenden nur μ und σ verwendet):

Substituiert man nun den Exponenten gemäß

,

so erhält man den Erwartungsnutzen

.

Anmerkung 1: Bei anderen Nutzenfunktionen lässt sich diese Form des Sicherheitsäquivalents nur näherungsweise über Taylor-Approximationen herleiten.

Anmerkung 2: Substitution des Exponenten in der Erwartungsnutzenberechnung

Bei der Berechnung des Erwartungswerte des Nutzens bei exponentieller Nutzenfunktion und normalverteilten Ergebnisgrößen lässt sich die Substitution

durch folgende Umformung der rechten Seite herleiten:

Anwendung auf lineare Entlohnungsfunktionen

Diese Berechnung des Sicherheitsäquivalents lässt sich auch auf Nutzenfunktionen von Ergebnissen bzw. Entlohnungen mit fixen und variablen Bestandteilen sowie Arbeitsleid übertragen. Dies wird insbesondere im LEN-Modell ausgenutzt. Dort wird für den Agenten ebenfalls eine exponentielle Nutzenfunktion uA mit normalverteilter Ergebnis- bzw. Entlohnungsgröße unterstellt (vgl. Burr/Stephan/Werkmeister [Unternehmensführung 2011] xxx):

mit rA als Risikoaversionskoeffizien, als Arbeitsleidfunktion und als lineare Entlohnungsfunktion des Agenten mit dem Prämienfaktor v für die erfolgsabhängige Entlohnung und dem Fixum f. Dann gilt für das Sicherheitsäquivalent SÄ des Agenten:

.

Dies lässt sich ohne Weiteres durch eine entsprechende Exponentensubstitution herleiten. Bemerkenswert ist lediglich, dass der Prämienfaktor v auch die Varianz des Ergebnisses beeinflusst und daher in die Risikoprämie eingeht.

___
siehe auch:
Christensen/Feltham: Economics of Accounting I: Information in Markets. Boston et al. 2003, S. 54f.; Burr/Stephan/Werkmeister: Unternehmensführung. 2. Aufl., München 2011.