Financial Resources Formulary: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| (4 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 82: | Zeile 82: | ||
* '''Stock price P<sub>0</sub> in the single-period case:''' [[Datei:Form_P0_einperiodig.png]] | * '''Stock price P<sub>0</sub> in the single-period case:''' [[Datei:Form_P0_einperiodig.png]] | ||
* '''Dividend discount model''' for the stock price P0 in the multi-period case until time horizon H: [[Datei: | * '''Dividend discount model''' for the stock price P0 in the multi-period case until time horizon H: [[Datei:cw_DDM_v2.png]] | ||
* '''Stock price P<sub>0</sub>''' with specific dividends until time horizon H and growing dividends after H: [[Datei:Form_P0_growth.png]] | * '''Stock price P<sub>0</sub>''' with specific dividends until time horizon H and growing dividends after H: [[Datei:Form_P0_growth.png]] | ||
| Zeile 165: | Zeile 165: | ||
== Exercises == | == Exercises == | ||
[[Financial Exercises | Please try our [[Financial Exercises]] or have a look at the [[Financial Ratios]] or at our [[Investition|investment pages]].<br/> | ||
[[Financial | |||
Aktuelle Version vom 14. Mai 2012, 10:08 Uhr
by Clemens Werkmeister
Present values, perpetuities and annuities
Present value PV: value of a future payment Ct (in year t), discounted to year 0: ![]()
Future value FVt: value of a present payment (in year 0), calculated by compounding to year t: ![]()
- t year
- r discount rate (interest rate)
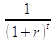 discount factor with discount rate (interest rate) r for t years
discount factor with discount rate (interest rate) r for t years- Ct cash flow in year t
- C0 initial investment of a project (for normal investment projects: C0 < 0)
- T number of years of the project
The sum of several present values is a PV, too (additivity of present values):![]()
Net present value NPV: PV of future payments (of a project or a company) plus the - usually negative - initial investment C0: ![]()
Perpetuity (console): a periodic (annual) payment C that is received or paid forever (beginning with the first payment at the end of year 1):![]()
Annuity: a payment of a level cash flow C during a specified number of years (from year 1 to n). Its present value can be calculated as difference between two perpetuities: ![]()
Annuity (recovery) factor: average payment at the end of n periods, corresponding to a present value PV and considering for interest rate r:![]()
Annuity present value factor: factor for the PV of n equal payments at the end of years 1 to n: ![]()
The annuity C for years 1 to n corresponding to a present value PV and discount rate r is: ![]()
Growing perpetuity: a perpetuity starting with cash flow C1 in year 1 and increasing by the annual growth rate g forever:![]() (for t = 1, 2, …, ∞ ;g < r) and
(for t = 1, 2, …, ∞ ;g < r) and ![]()
Growing annuity: an annuity starting with cash flow C1 in year 1 and increasing by the annual growth rate g for n years: ![]() (with t = 1, 2, …, n)
(with t = 1, 2, …, n)
Internal rate of return (IRR): discount rate that results in NPV = 0: ![]()
Profitability index: ratio of NPV to investment of a project: ![]()
Equivalent annual cash flow (EAC): cash flow per year with the same present value as the actual cash flow of the project: 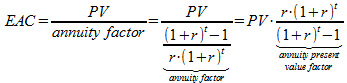
Interest and discount rates
Effective annual rate (EAR): annualized rate of shorter period interest rates (monthly, daily rates) using compound interest:
- - EAR for a monthly rate m: EAR = (1+m)12 – 1
- - EAR for a daily rate d: EAR = (1+d)360 – 1 (for 360 days per year)
Given an annual percentage rate (APR) of r, the corresponding EAR with respect to n shorter periods of equal length is: ![]()
Effective annual rate with continuous compounding: effective annual rate for n → ∞ shorter periods: ![]() (being r the simple annual rate)
(being r the simple annual rate)
Annual percentage rate (APR) or simple rate: annualized rate of shorter period interest rates (monthly, daily rates) using simple interest.
- - APR for a monthly rate m: APR = 12 * m
Real rate of return: rate of return adjusted for inflation: ![]() →
→ ![]() (being i the inflation rate)
(being i the inflation rate)
Valuing bonds
- Ct annual coupon interest payment
- F face value (or principal)
- r discount rate (yield to maturity)
- N maturity
Duration of a bond with maturity N: weighted average period of bond payments: 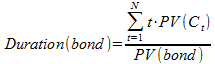
Modified duration: a measure of volatility (elasticity) of bond prices: ![]()
Valuing stocks
(Expected) Stock return r (equity cost of capital): ![]()
Present value of growth opportunities (PVGO): net present value of a firm's future investments.
Return (Equity cost of capital) of a perpetual stream of dividends with growth: ![]()
Return on Equity with market values: ![]()
Payout ratio: fraction of earnings paid out as dividends: ![]()
Plowback ratio: fraction of earnings retained by the firm: ![]()
Sustainable growth rate: rate at which a firm can steadily grow: 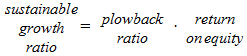
Discounted cash flow (DCF): value of the free cash flows that are available to investors plus company value at the planning horizon, all discounted to present: ![]()
Risk and return
Risk premium of an asset: asset return – return of risk-free asset.
Variance: expected value of squared deviations of observations from their expected value (mean): ![]() (based on j observations)
(based on j observations)
Standard deviation: a measure of volatility of expected stock returns: ![]()
Expected portfolio return (with two assets): ![]()
Expected portfolio return (with j = 1, …, n assets): ![]()
- xj weight of asset j in the portfolio
- rj (expected) return of asset j
Variance of portfolio return (portfolio variance) in the case of two assets: ![]()
Covariance between asset i and j with ![]()
Correlation coefficient between asset i and j: ![]()
Variance of portfolio return (portfolio variance) in the case of n assets: ![]()
Sharpe-Ratio: ratio of risk premium to risk (standard deviation): ![]()
Beta of the return of asset j to the market return (return of market portfolio m): ![]()
Expected return following the security market line equation (SML): ![]()
Expected return of a stock in event studies: ![]()
Abnormal return = actual return – expected return = ![]()
Capital Structure and Return
Weighted average cost of capital (WACC): ![]()
- rD interest rate on debt resp. debt cost of capital
- rE return on equity resp. equity cost of capital
- Tc corporate tax rate
Weighted average cost of capital (WACC) with a zero-tax rate: ![]()
Leverage-formula for return on equity: return on equity increases with debt/equity-ratio: ![]()
Leverage-formula for equity beta: risk increases with debt/equity-ratio: ![]()
Exercises
Please try our Financial Exercises or have a look at the Financial Ratios or at our investment pages.