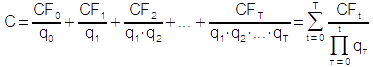Kapitalwert
von Clemens Werkmeister
Idee des Kapitalwerts
Der Kapitalwert ist eine monetäre Kennzahl zur Beurteilung einer Investition. Inhaltlich misst der Kapitalwert den Wertzuwachs, der durch ein Investitionsprojekt im Vergleich zu seiner Unterlassung entsteht. Im Allgemeinen wird der Kapitalwert auf den Entscheidungszeitpunkt bezogen (Periode 0). Spätere Einzahlungen oder Auszahlungen werden auf diesen Zeitpunkt abgezinst. Das Standardvorgehen setzt bestimmte Anlage- und Finanzierungsalternativen voraus. Diese sind insbesondere auf einem vollkommenen Kapitalmarkt gegeben. Bei unvollkommenen Kapitalmärkten ist die Berechnung und Interpretation des Kapitalwerts anzupassen.
Grundlage der Kapitalwertberechnung sind die prognostizierten Zahlungen zukünftiger Perioden. Fallen zu einem Zeitpunkt bzw. in einer Periode mehrere Einzahlungen und Auszahlungen an, werden diese zunächst saldiert und anschließend auf die Periode 0 abgezinst (diskontiert). Der Saldo wird als Einzahlungsüberschuss (auch Einnahmenüberschuss oder Cash Flow) bezeichnet.
Der auf die Periode 0 abgezinste Wert einer späteren Zahlung heißt Barwert. Der Kapitalwert ergibt sich als Summe aller Barwerte der Zahlungen eines Projekts von der laufenden Entscheidungsperiode 0 bis zum Projektende.
Als Ertragswert wird (beispielsweise in der Unternehmens- oder Immobilienbewertung) die Summe der diskontierten zukünftigen Cash Flows bezeichnet (also von Periode 1 bis zum Ende des Projekt- oder Planungshorizontes).
Berechnung des Kapitalwerts
Die Standardform der Kapitalwertberechnung
In der Standardform wird der Kapitalwert C eines Projekts berechnet als Summe der Barwerte BWt des Überschusses der Einnahmen Et über die Ausgaben At in den Projektperioden t. Zur Diskontierung dient der Zinssatz i bzw. der Zinsfaktor q = 1+i. Andere gebräuchliche Variable für den Zinssatz sind r, p oder gelegentlich auch k.
Berechnung von Barwert und Kapitalwert
Für den Barwert BWt eines Einnahmenüberschusses in Periode t gilt:
Üblicherweise wird zur Barwertberechnung auf Periode 0 abgezinst. Eine Abzinsung auf andere Perioden wäre ggf. zu kennzeichnen.
Der Kapitalwert wird dann standardmäßig wie folgt berechnet:
Durch Aufzinsung des Barwerts oder Kapitalwerts auf den Zeitpunkt T erhält man den Endwert.
Kapitalwertfunktion
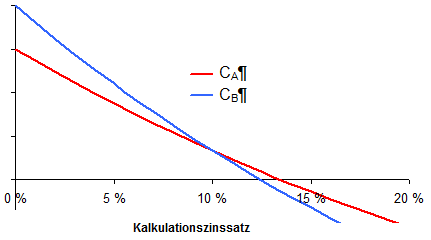
Aus der Berechnung ergibt sich unmittelbar die Bedeutung des Kalkulationszinssatzes für den Kapitalwert. Sie wird in der Kapitalwertfunktion C(i) betont und hängt von den Cash Flows ab. Für ein Normalprojekt, das mit einer Auszahlung beginnt, auf die mehrere Einzahlungen folgen, fällt die Kapitalwertfunktion mit steigendem Kalkulationszinssatz. Für zwei Projekte A und B sehen die Kapitalwertfunktionen dann typischerweise wie folgt aus:
Beim internen Zinssatz nimmt die Kapitalwertfunktion den Wert null an. Dieser kann die Entscheidung für ein Projekt im Vergleich zu seiner Unterlassung vereinfachen, da ein solches Normalprojekt nur für Kalkulationszinssätze unterhalb des internen Zinssatzes vorteilhaft ist. Entsprechend größere Ungenauigkeiten bei der Prognose des Kalkulationszinssatzes können dann hingenommen werden, solange davon ausgegangen wird, dass er unter dem internen Zinssatz bleibt.
Für den Vergleich mehrerer Projekte (hier eine Auswahlentscheidung zwischen A und B) ist jedoch der Schnittpunkt ihrer Kapitalwertfunktionen interessanter: Bei Kalkulationszinssätzen unterhalb des Schnittpunktes ist Projekt B vorteilhaft, bei Zinssätzen darüber ist es Projekt A, sofern überhaupt noch positive Kapitalwerte vorliegen.
Sofern Projekte zu beurteilen sind, bei denen mehrere Einzahlungen und mehrere Auszahlungen sich abwechseln, verliert die Kapitalwertfunktion jedoch ihre heuristische Funktion, da sie bei unterschiedlichen Zinssätzen mehrere lokale Hoch- oder Tiefpunkte aufweisen kann.
Kapitalwertberechnung bei periodenspezifischen Zinssätzen
Liegt für jede Periode ein unterschiedlicher Kalkulationszinssatz it vor, ist der Cash Flow von jeder Periode t zur Vorperiode t-1 mit einem anderen Zinssatz bzw. Zinsfaktor qt abzuzinsen. Für den Kapitalwert gilt (unter Verwendung des Produkt-Operators):
Ein Beispiel zur Diskontierung findet sich hier.
Kapitalwertberechnung einer unendlichen Rente
Eine zusammenhängende Folge von Zahlungen in gleichen Zeitabständen und gleicher Höhe heißt in der Investition und Finanzierung auch Rente. Sofern es sich um eine endliche Folge solcher Zahlungen handelt, spricht man von einer Annuität, eine unendliche Folge wird als ewige Rente (oder Perpetuity bzw. Console) bezeichnet. Üblicherweise wird die erste Rentenzahlung auf das Ende des Jahres 1 gesetzt (nachschüssige Rente), in manchen Fällen auch auf den Beginn des ersten Jahres bzw. das Ende des Jahres 0 (vorschüssige Rente). Der Kapitalwert C einer ewigen (nachschüssigen) Rente in Höhe von CF ist für einen Kalkulationszinsatz i:
C = CF/i.
Dies lässt sich folgendermaßen herleiten: Der Kapitalwert in Jahr 0 entspricht dem Kapitalwert der ewigen Rente in Jahr 1 zuzüglich dem Cash flow des Jahres 1, beides abgezinst um ein Jahr:
C0 = (C1 + CF1)/(1+i) bzw. (1+i) ∙ C0 = C1 + CF1
Da für eine unendliche Rente C1 = C0 gilt, vereinfacht sich dieser Ausdruck auf C0 = CF1/i.
Der Wert einer vorschüssigen Rente ist um den Faktor (1+i) höher als der einer gemeinhin unterstellten nachschüssigen Rente gleichen Betrags.
Kapitalwertberechnung einer wachsenden Rente
In vielen Fällen werden zusammenhängende Folgen von Zahlungen in gleichen Zeitabständen beobachtet, deren Betrag von Zahlung zu Zahlung ansteigt. Gründe dafür sind beispielsweise Preiserhöhungen oder Tarifsteigerungen. Sofern der Anstieg mit einer gleichbleibenden Wachstumsrate g erfolgt, spricht man auch von einer konstant wachsenden Rente. Soweit es sich um eine ewige Rente mit konstantem Wachstum handelt, ist zur Berechnung ihres Kapitalwerts der Nenner um die Wachstumsrate g zu korrigieren:
C = CF/(i-g).
Die Anwendung dieses Ausdrucks ist nur unter der Annahme sinnvoll, dass der Kalkulationszinssatz größer als die Wachstumsrate der Cash Flows ist (i>g). Während für einen begrenzten Zeitraum ein Wachstum der Cash Flows über dem Kalkulationszinssatz, sprich den Opportunitätskosten des Kapitalmarktes, möglich ist, ist es für einen unendlichen Zeitraum nicht sinnvoll interpretierbar.
Kapitalwertberechnung bei stetiger Verzinsung
Vorwiegend für Anwendungen in investitions- und finanzierungstheoretischen Modellen ist es hilfreich, wenn keine periodenbezogene, sondern eine kontinuierliche (oder stetige) Verzinsung i unterstellt werden kann. Man spricht auch von der Momentanverzinsung oder Verzinsungsenergie. Der Kapitalwert C einer Zahlung CFt zum Zeitpunkt t berechnet sich dann zu
C = CFt ∙ e-i∙t.
Diese Beziehung lässt sich als Grenzfall einer unterjährigen Verzinsung für unendliche viele Verzinsungsperioden herleiten.
Anwendung des Kapitalwerts
Verbreitete Anwendungen des Kapitalwerts sind die Beurteilung von Investitionsprojekten und die Unternehmensbewertung. Dort erlaubt die Kapitalwertberechnung eine isolierte Projektbeurteilung, die alternative Anlagemöglichkeiten pauschal über den Kalkulationszinssatz erfasst.
Bei der Beurteilung von Investitionsprojekten gilt ein Projekt als vorteilhaft, wenn der Kapitalwert positiv ist. Beim Vergleich mehrerer, sich ausschließender Projektalternativen (Auswahlentscheidung) ist die Alternative mit dem höchsten Kapitalwert vorteilhaft. Bei der Entscheidung über mehrere Investitionsprojekte, die sich teils ergänzen, teils auch ausschließen können (Investitionsprogrammentscheidung), sind die Kapitalwerte alternativer Investitionsprogramme zu bestimmen und zu vergleichen.
In der Unternehmensbewertung finden sich verschiedene Varianten der Kapitalwertmethode als Discounted-Cash-Flow-Methoden (DCF-Methoden).
Vorteile des Kapitalwerts
Zentraler Vorteil des Kapitalwerts ist die Möglichkeit der differenzierten Erfassung und Bewertung künftiger projektbezogener Zahlungen, die zu unterschiedlichen Zeitpunkten in unterschiedlicher Höhe anfallen. Dabei können die Zahlungen direkt bewertet werden, d.h. ohne den Umweg über kalkulatorische Größen (insbesondere Abschreibungen oder Rückstellungen), wie sie im externen Rechnungswesen oder in der Kosten- und Leistungsrechnung üblich sind.
Die Kapitalwertmethode ist einfach nachzuvollziehen und in zahlreichen Softwarepaketen standardmäßig verfügbar. Sie erlaubt einfache Vorteilhaftigkeitsaussagen, die auf Prognosen künftiger Werte basieren und sich somit grundsätzlich von vergangenheitsorientierten Bewertungen lösen.
Nachteile des Kapitalwerts
Generell beruht die Aussagekraft des Kapitalwerts auf der Verfügbarkeit der unterstellten Kapitalmarktbedingungen und der Verlässlichkeit der zugrundeliegenden Cash-Flow-Prognosen. Die Vorteilhaftigkeit eines Projekts hängt in hohem Maße von den unterstellten Kalkulationszinssätzen ab. Auch durch die Prognose der Einnahmenüberschüsse können die Vorteilhaftigkeit eines Projekts oder der Unternehmenswert beeinflusst werden.
Spezielle Probleme weist der Kapitalwert auf, wenn in Timing-Problemen Investitionsketten aus Projekten unterschiedlicher Laufzeiten zu beurteilen sind. In bestimmten Fällen ist dann die Annuität das bessere Kriterium.
--
siehe auch:
- Financial Exercises 1: Discounting and compounding
- Financial Exercises 2: PV and Annuity
- Financial Exercises 3: NPV and IRR
___
siehe auch:
Kruschwitz, Lutz: Investitionsrechnung. 14. Aufl., Berlin 2014.
Troßmann, Ernst: Investition als Führungsentscheidung. 2. Aufl., München 2013.
Troßmann, Ernst / Baumeister, Alexander / Werkmeister, Clemens: Fallstudien im Controlling. 3. Aufl., München 2013.